Computer Science
Computer science teaches students how to approach problems from an algorithmic perspective, how to understand the nature and broad reach of computation, and how to apply that knowledge abstractly.
Math, Data, & Computation
Why is mathematics considered the language of science? Do today's discoveries in math, data science, and computation provide frameworks for the science and technology of tomorrow?
Explore Math, Data, & Computation
Explore areas of study in mathematics, data science, and computation to deepen our understanding of complex systems, improve processes, and foster advancements in technology and innovation.
Data Science
Data science concerns principles and methods applied in a broad array of activities spanning data collection, storage, integration, analysis, inference, reasoning, reporting, and ethics.
Mathematics
Mathematics studies the concepts of quantity and number, geometry and shape, and functions and change. It provides an approach to problem solving which emphasizes abstraction as a key tool.
Statistics
Statistics is the scientific discipline that deals with the collection, organization, analysis, display, and interpretation of numerical data. Statistical methods are widely used to collect information about the world.
Interesting Courses
Check out some examples of courses that unravel the fascinating world of math, data, and computation.
STAT 302
How can we turn raw data into compelling stories?
STAT 370
Can statistics tell us about human suffering and injustice?
MATH 327-0
How does math reveal the rules of motion and conservation?
MATH 220-2
How can calculus uncover areas, volumes, and infinite behaviors?
PSYCH 201
How do hidden psychological forces shape our political beliefs and actions?
SOCIOL 303-0
Can we trust numbers to reveal the truth about society, or are they biased?
NEUROSCI 390-0-28
Can math unlock the secrets of the brain and pave the way for smarter machines?
POLI_SCI 312-0
Can we measure racism, political conflict, and colonialism using numbers?
BIOL_SCI 337
Can mastering statistics help us unlock the secrets of the natural world?
What is it like to be a student?
As a student, you can delve into the study of math, data, and computation through interdisciplinary coursework, internships, community projects, and extra-curricular activities. You also can collaborate with faculty on cutting-edge research.
Nia Robles Del Pino ‘24
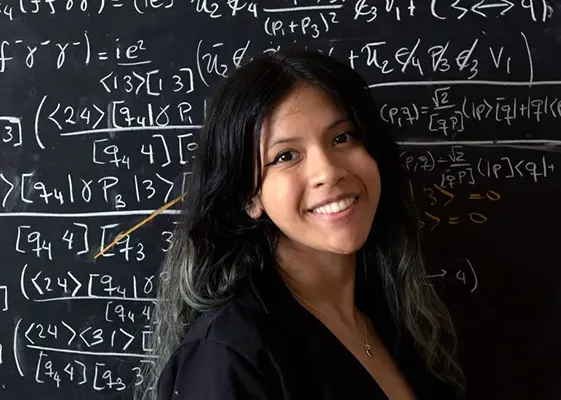
The 2024 Global Rhodes Scholar was a double major in mathematics and physics. At Northwestern, Robles Del Pino immersed herself in Quantum Field Theory. With a focus on high-energy particle theory research, she worked as an undergraduate researcher in the group “Amplitudes and Insights” led by physics professor John Joseph Carrasco. She also completed an independent study project on Spinor Helicity Variables and Quantum Chromodynamics and an honors thesis on supergravity theories.
Innovators in the Classroom and Beyond
Get to know some of our dedicated professors who are passionate about teaching and nurturing your success as a student.
Arend Kuyper shares how data sciences empower students to solve future challenges
Professor Arend Kuyper reveals how, in a data-driven world, students' ability to analyze and communicate insights is a game-changing skill. Northwestern's unique liberal arts approach fosters critical thinking, communication, and collaboration across disciplines, preparing students to thrive in any field.
Bryna Kra describes how mathematics is a dynamic field fueling innovations in AI and other industries
Professor Bryna Kra explains that math is an ever-evolving field driving innovations in AI and other industries. She highlights opportunities for undergrad research and interdisciplinary collaboration, as well as the versatility of the math major, which pairs with other subjects to open a wide range of career paths.
Eric Zaslow teaches “horizontal” connections across subjects
The Henry Sanborn Noyes Chair in Mathematics rejects the vertical, hierarchal course progression you find in most mathematics programs. He teaches students to explore concepts horizontally, which is critical to real thinking.
Shaping the Future of Math, Data, & Computation
Xiumin Du
Mathematics
Professor Du’s research interest lies in harmonic analysis and its interactions with geometric measure theory and partial differential equations (PDEs). A key idea behind harmonic analysis is to express a general function or operator as a sum of simpler parts. Harmonic analysis has countless applications in signal processing, tomography and quantum mechanics, among other areas.
Aaron Naber
Mathematics
Aaron Naber, Kenneth F. Burgess Professor of Mathematics, is a geometric analyst working on the regularity, singularity, and topology of geometrically motivated equations. Naber’s well-known works include the proof of the codimension four conjecture for Einstein manifolds, a disproof of the Milnor conjecture, and a proof of the energy identity conjecture. Together with collaborators, he built a structure theory for the singular sets of various nonlinear equations, including nonlinear harmonic maps and spaces with lower Ricci curvature bounds.
Ananth Shankar
Mathematics
Shankar’s research is in number theory and arithmetic geometry, focusing mainly on Shimura varieties and abelian varieties. He studies the arithmetic of polynomial equations and their solutions. Shimura varieties are geometric spaces that are defined as solutions to polynomial equations with rational coefficients. Shimura varieties have played a crucial role in settling several long-standing conjectures, including the Mordell conjecture.
Outside the Classroom
Explore student clubs, internships, and campus resources.
Weinberg in the World Podcast
In Weinberg College's monthly podcast, alumni share their career experiences. Discover stories about working in fields related to math, data and computation.
Career Talk Event with Junta Nakai '04: Global Industry Leader at Databricks
May 7, 2020
Junta Nakai highlights his transition from finance to Databricks, a company that specializes in big data and AI, tools that rely heavily on computational models to predict trends and drive decision-making in industries like finance. His work at Databricks involves leveraging data and machine learning technologies to redefine financial services, illustrating the vital role of data-driven computation in shaping the future of business.
Career Conversation with Mai Sistla '14: Deputy Director at the Aspen Tech Policy Hub
January 26, 2023
Weinberg grad Mai Sistla '14 discusses her journey from Northwestern to deputy director at the Aspen Tech Policy Hub. Learn about important classes, extracurriculars, grad school, and the value of an Arts & Sciences education.
STAT 302
Data Visualization
About the Course
Introduction to the knowledge, skills, and tools required to visualize data of various formats across statistical domains and to create quality visualizations for both data exploration and presentation.
STAT 370
Human Rights Statistics
About the Course
Development, analysis, interpretation, use, and misuse of statistical data and methods for description, evaluation, and political action regarding war, disappearances, justice, violence against women, trafficking, profiling, elections, hunger, refugees, discrimination, etc.
MATH 327-0
Mechanics for Mathematicians
About the Course
Fundamental mathematical ideas arising in classical mechanics: Newtonian mechanics, Lagrangian formalism and the calculus of variations, motion with constraints, symmetries and conservation laws, Hamiltonian mechanics, and Liouville's theorem.
MATH 220-2
Single-Variable Integral Calculus
About the Course
Definite integrals, antiderivatives, and the fundamental theorem of calculus. Transcendental and inverse functions. Areas and volumes. Techniques of integration, numerical integration, and improper integrals. First-order linear and separable ordinary differential equations.
PSYCH 201
Statistical Methods in Psychology
About the Course
These questions all concern the psychological foundations of political phenomena in everyday life. Determining the psychological factors that drive people's political attitudes and behaviors have long been a central question in understanding everyday human behavior, and remains so today. This seminar-based course will cover foundational topics in the psychology of politics, including the psychological profiles of liberals and conservatives, morality, political behavior (e.g., voting), social stability and change, and stereotyping and prejudice.
SOCIOL 303-0
Analysis and Interpretation of Social Data
About the Course
This course introduces statistics and data analysis for the social sciences, focusing on interpreting and using data to understand the social world. It starts by encouraging critical analysis of everyday data and empirical analyses from policy and journalism. The second part covers basic statistical analysis, where students collect, analyze, and interpret data. The course also explores how computation, including machine learning, shapes modern social understanding.
NEUROSCI 390-0-28
Brain Function Through the Lens of Computation
About the Course
Understanding brain function is a grand challenge for twenty-first century science that promises revolutionary applications to medicine and artificial intelligence. Mathematical modeling can contribute valuably to this understanding by allowing scientists to formalize experimental findings and reason beyond their intuition.
POLI_SCI 312-0
Statistical Research Methods
About the Course
How racist is the average American, and what makes some more racist than others? Why can't Democrats and Republicans just get along? Does a country's colonial experience shape its future political and economic possibilities? These questions, and many more, have been addressed by statistical research in political science. This course explores quantitative/statistical research methods in the social sciences, with the goal of helping students learn how to carry out statistical social science research of their own. To that end, we will review the basics of statistical theory and quantitative research design. We will also examine applications of these methods to various topics in political science. Throughout, the emphasis will be on practical, applied advice for constructing and successfully completing quantitative research in political science and related fields.
BIOL_SCI 337
Biostatistics
About the Course
This is a statistics class geared toward students interested in biology, ecology, and environmental science, but others are welcome. The course is applied statistics with the goal of students being able to use the skills, experience, information, and software learned in class after class.